This is a description of an emblem, a vivid and possibly surreal image, with various associated meanings. I think that deliberately crafting emblems for oneself is possibly useful (I have written about the project in a post called "Deliberately creating mental-entities; chunks"), but certainly fun.
Millefiori
There is a technique, which was probably reinvented at various times and places over the world, but which is currently associated with the craft Venetian glass and polymer clay, of creating a fine pattern by first creating it at a large and crude scale in a short and fat cane, then reducing the cane until it is long and thin, then possibly using that finely detailed cane, either in another cane, or in a final product.
This is a concrete and vivid metaphor for abstraction. There are two parts to an abstraction. The first part is the "def". In mathematics, a def is a statement and proof of a named theorem or lemma. In programming, a def is often a function declaration and definition (or the declaration and definition of another kind of abstraction, but functions are one of the most common). In Millefiori, a def is the construction and reduction of a cane.
The second part is the "use". In mathematics, a use is referencing a applying a previously-established named theorem or lemma in another proof. In programming, a use is invoking a function that has been declared and defined elsewhere. In Millifiori, a use is cutting a length of a reduced cane, maybe a thin disc or a short segment, and using it, either in a final piece or in another cane.
There are two opposite transformations that one can make. In refactoring, which is a part of programming, they might be called inlining and extracting. In proof theory, which is a corresponding part of mathematics, specifically logic, they might be called cut introduction and cut elimination.
In the domain of Millefiori, if you have a procedure where you use 5 solid-color canes to make an intermediate cane, and then you use 3 copies of that cane to make a final cane, then you might have instead carefully, delicately built the final cane directly out of 15 solid-color canes. This is "inlining". Inlining transforms a use-def pair into nothing, like matter-antimatter collisions. Alternately, if you have a complex shape that you want to make, such as a flower or a fish, then you might look for substructures - recurring clusters or patterns that appear multiple times within the target shape, such as a petal, leaf, scale, or fin. Once you recognize those, you can revise your strategy for making the final shape. First build (once) a cane for the recurring substructure, and subsequently use that cane several times in constructing the complex shape. This is "extracting". Extracting transforms nothing into a use-def pair, like virtual particles appearing.
Names have power
True names are, in fiction, magically powerful (Eliot 1939, Le Guin 1964, Vinge 1981, Rothfuss 2007). Even in reality, one of the ways that we can use names is to gain a grip on something otherwise difficult to gain a grip on.
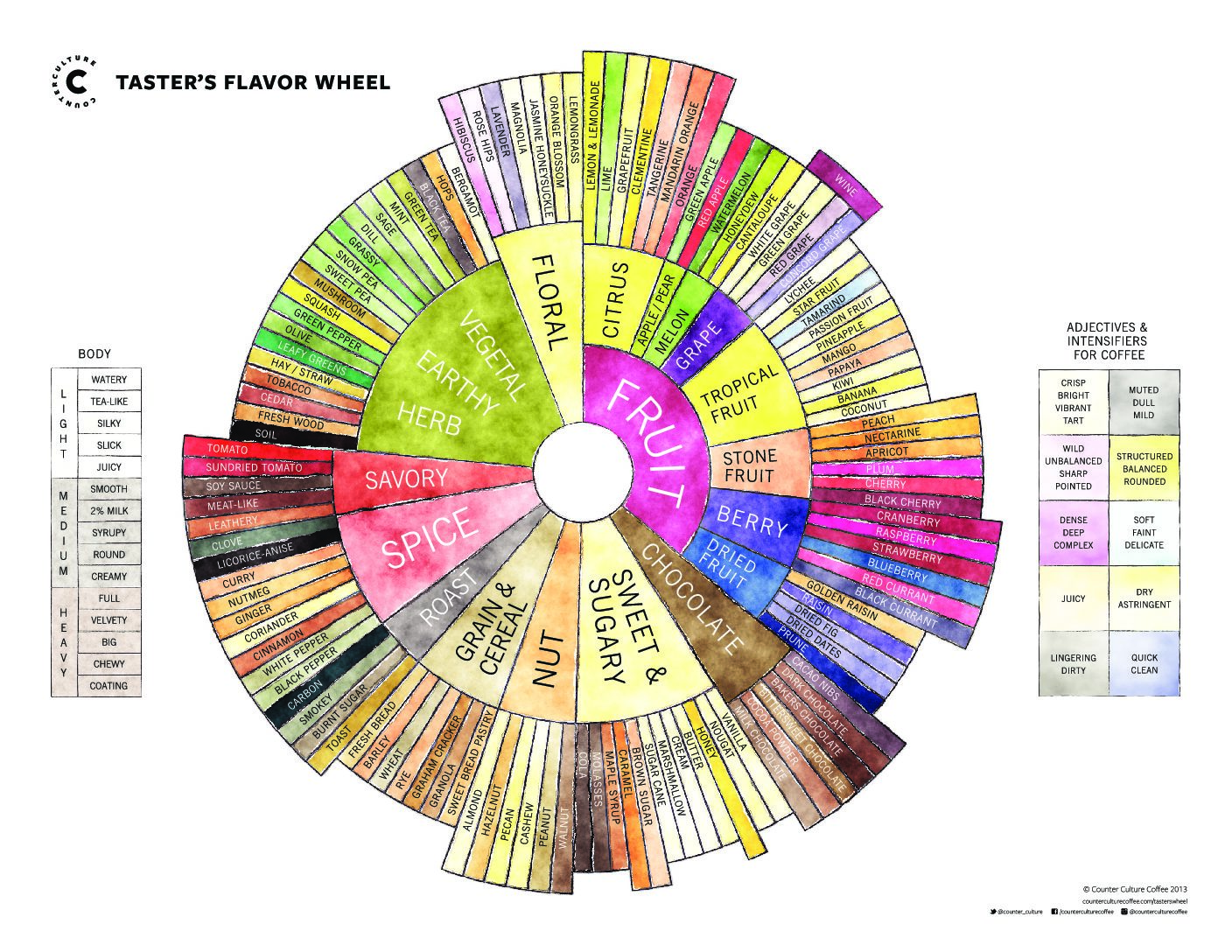
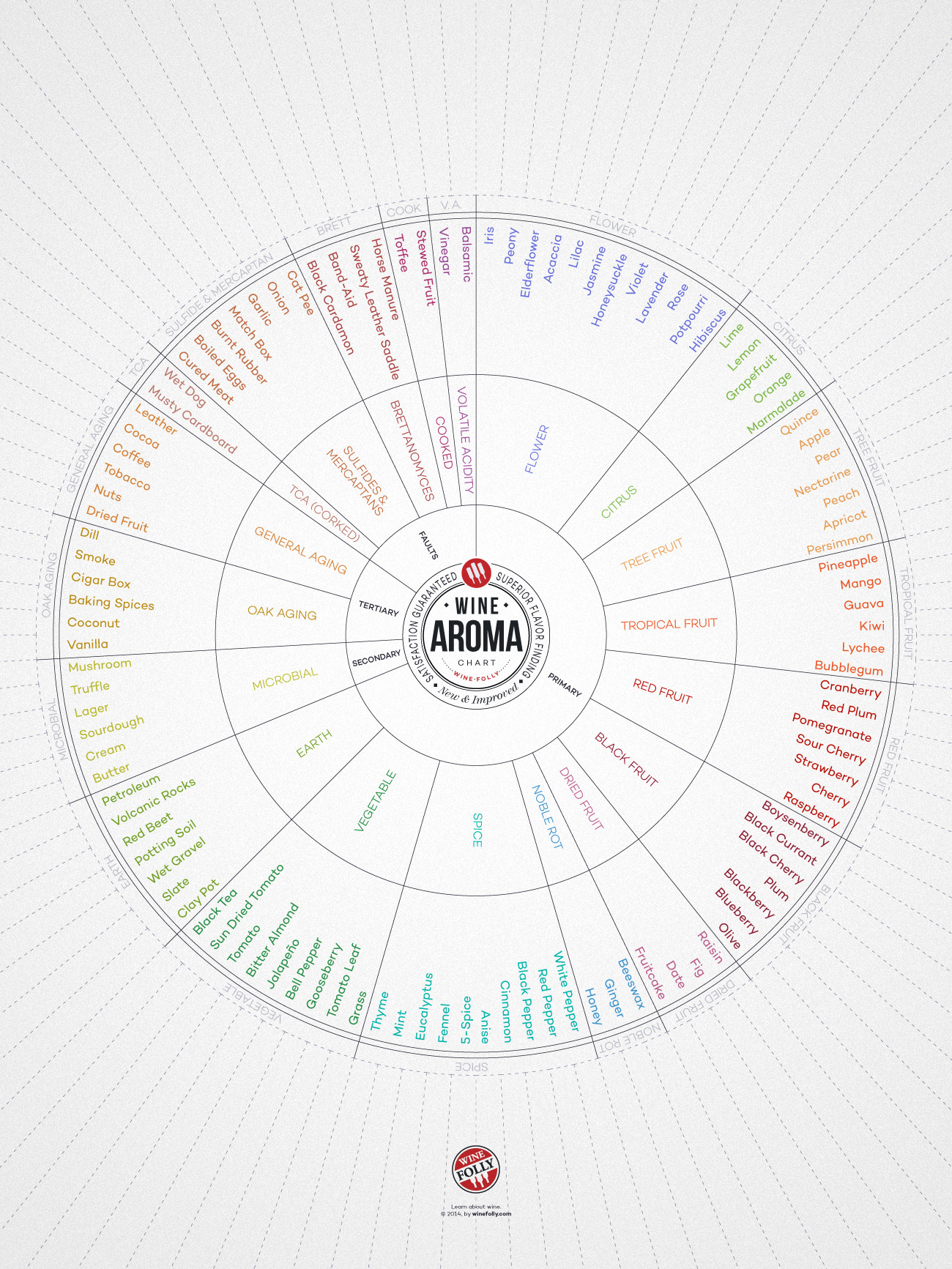
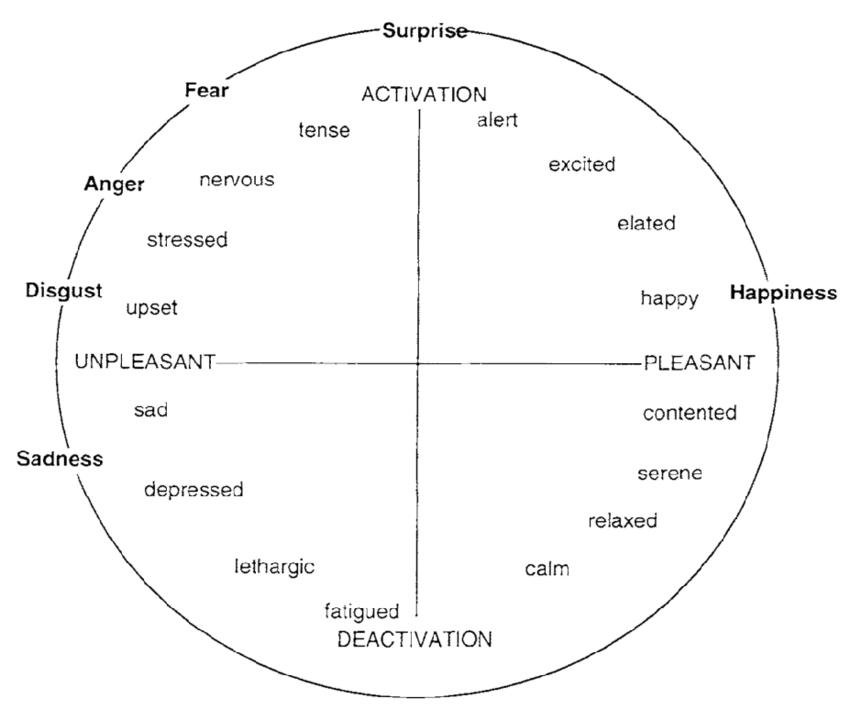
A "tasting notes diagram" for example, for coffee or for wine, encourages you to move your attention around to different names for tastes, and compare the nebulous taste that you are presently tasting to the taste denoted by the words. You may get a "mismatch", or a "match" or a "partial match". If you get a partial match, you may be able to turn your attention from the whole nebulous taste to the difference remaining after characterizing it, saying something like "It's a bit fruity, but also <remaining description>".
Similarly, something like the circumplex model of affect can act like a tasting wheel, allowing you to consider various names for emotions, and get a sense of "mismatch", "match", or "partial match".
Technical names can act as handles for applying fragments of domain knowledge
There are technical names for problems that can occur during particular processes. For example, in sand casting a "drop" is a kind of flaw - specifically, it is an irregularly shaped projection on the cope surface of a casting. It occurs when a chunk of sand at the top of a mould separates and falls. Knowing the word for the phenomenon might help someone perceive something precisely, not just the nebulous, slippery observation "my piece didn't turn out as nicely as I wanted". Furthermore the word links to some ideas about how it happens, leading to some ideas for what to do about it.
Similarly, names for debugging phenomena such as "Heisenbug" can allow programmers who might otherwise be flummoxed to recognize the phenomenon, and jump out of their usual habits, unsticking themselves. (A Heisenbug occurs when the measurement apparatus, such as a debugger or other harness, interacts with the mechanism of the bug, causing the bug to appear and disappear in the same circumstances as the programmer's attention on the bug.)
Creating your own names for things has power
In some cases, after you notice something, point to something, or focus your attention on something, you can find a pre-existing name for it. In other cases, you need to create your own term - even if you don't use that term for long, it can be helpful.
When Descartes wrote "The Geometry" he recommended a systematic method. As interpreted by Polya, his problem-solving method includes steps like "draw a diagram", "identify clearly what you are trying to find", and (crucially for this topic) "label the parts", including the known ones (Decartes used letters like A, B, C for knowns) and the unknown ones (Decartes used letters like x, y, z for unknowns, and this established the now widely-used convention), and "write down all known relationships among these symbolically". What I'm trying to say by borrowing Decartes and Polya's authority is that this tagging or labeling with lightweight names, like letters, is legitimately useful in solving problems.
A common recommendation in programming is whenever you find a sufficiently-repeated formula or block of code (such as twice-repeated, or thrice-repeated, depending on who is doing the recommending), you probably should give it a name. The slogan is DRY: Don't Repeat Yourself. It's hard to say why people recommend this, because they give different reasons. I suspect the real reason that people recommend DRY is that introducing names for things changes your thought process about those things, in a good way.
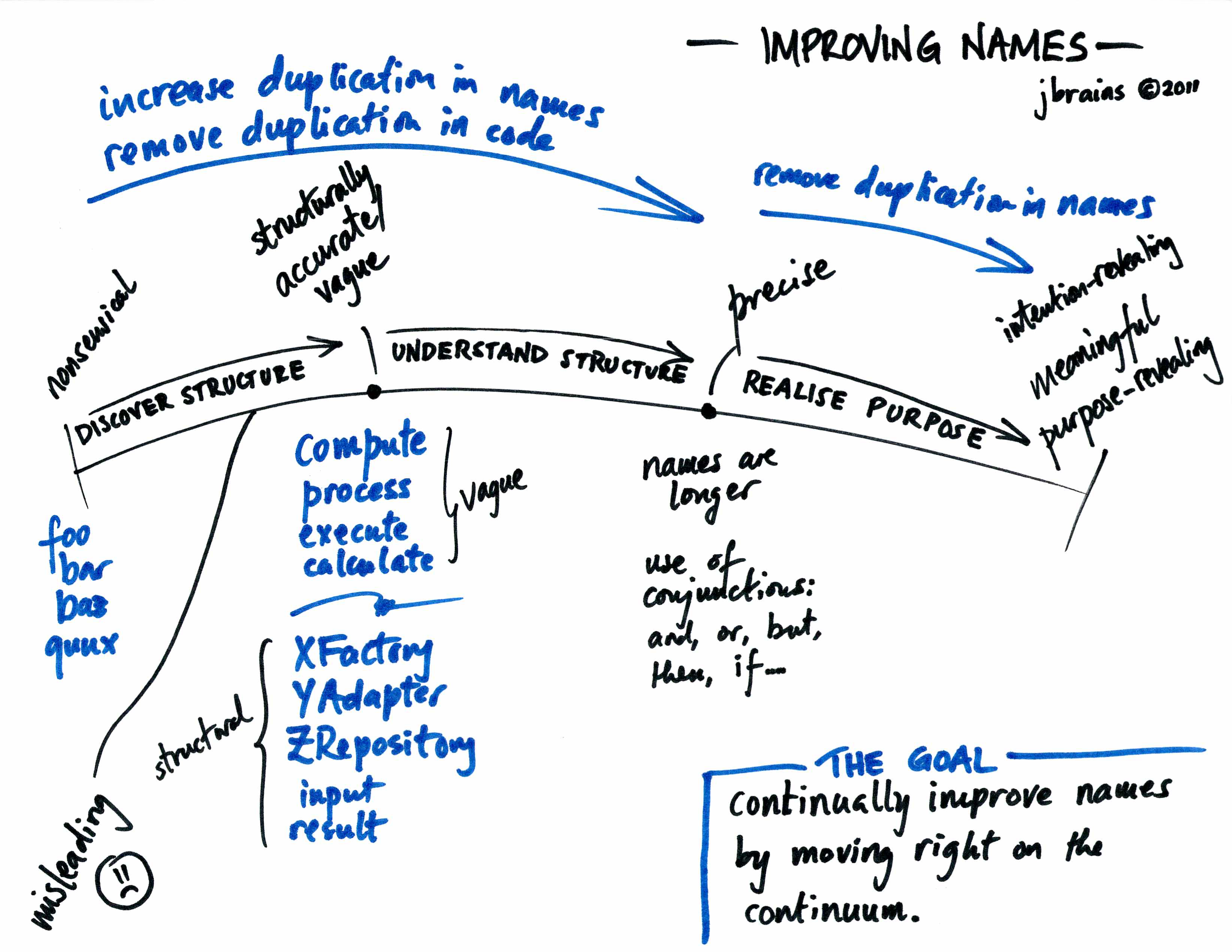
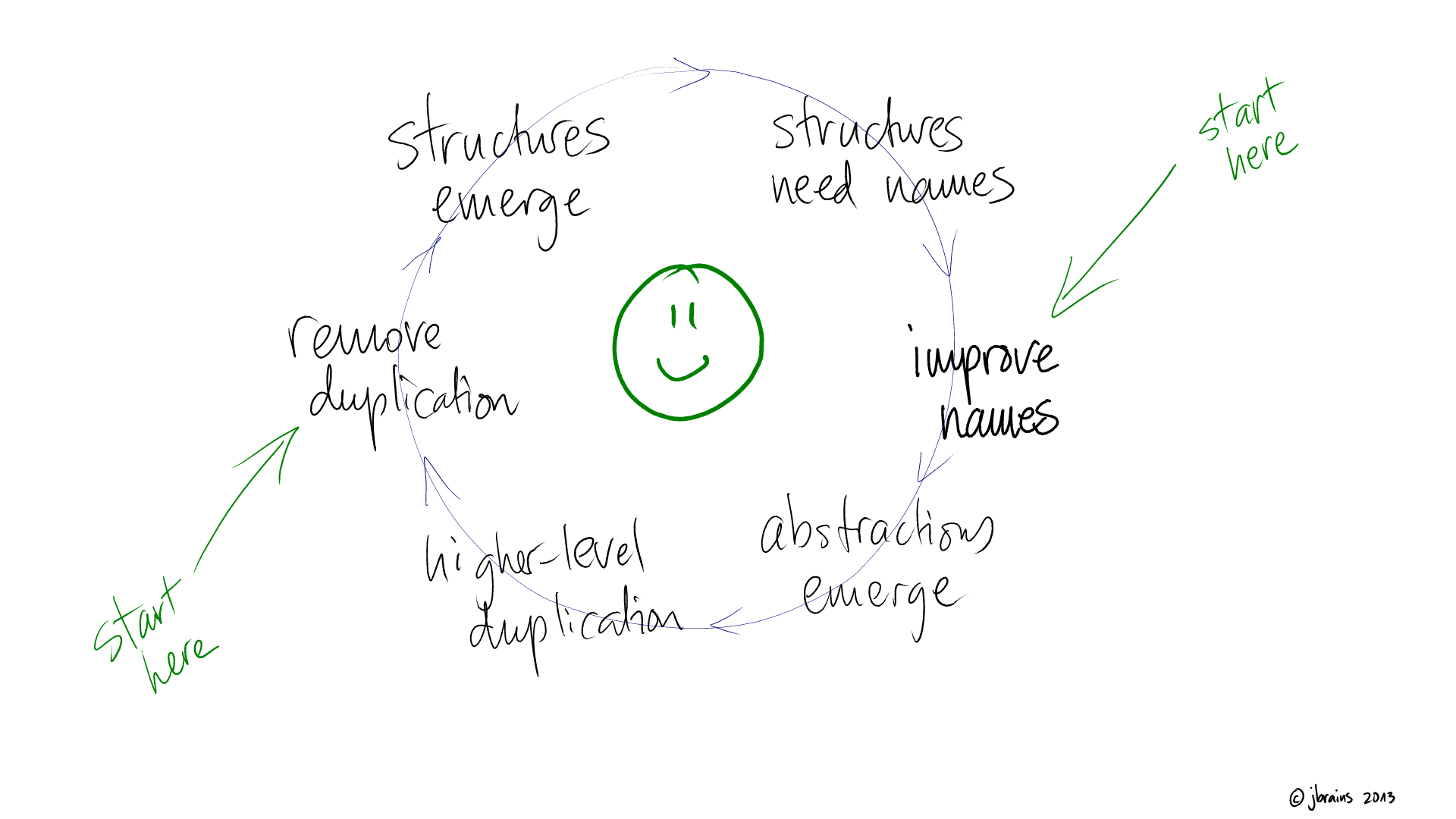
J.B. Rainsberger has a spiel about the process of naming things (in programming), with two associated diagrams:
Relatedly, Arlo Belshee has a similar spiel. Arlo Belshee's spiel is historically first, but also more verbose, and the two are probably somewhat independent, though also definitely aware of one another.
To summarize these two spiels, they're about the gradual process of naming things in programming.
- Names can start meaningless - going from pointing to an unnamed repetition to calling something "foo" or "x" is progress.
- Changing something's name from meaningless to a name that captures some structure of the thing is also progress.
- It's okay for the name to initially be a bit vague, and only have some aspect of its structure in its name. Some "computery" names like "XFactory", "YAdapter", "ZRepository", "input", or "result" are vague-but-structural in this manner.
- You can rename it to include more of its structure in the name, and this is also progress.
- Eventually you have captured all of what something is in its name, at which point the name might be quite long, like Tolkein's Entish. This precision is progress, and it is fine at this point for the name to contain conjunctions.
- Eventually, you may understand not just the thing being named but also the context of the thing well enough to rename the thing after the purpose or role that it plays in that context, which can often be shorter and clearer to read when the thing is being used - and most things are used more often than they are defined, so that is progress.
I don't have great examples of using the power of creating your own names for things in the realm of emotions or personal experience. However, Gendlin's Focusing, if I understand correctly, is a technique of taking initially-unnamed "felt senses" and putting words or names to them. Lippman's Protocol 1 (which I don't understand in detail) contains a long list of names of auxiliary practices. which makes me think that naming things is a good idea or recommended by experts.
D.R.MacIver has written about creating an idiosyncratic distinction between anxiety and worry. This illustrates a few different things. One is that your own personal names for things don't have to be wildly novel, as if they were picked from an Orcish name generator: "Ughash", "Baghig", "Xomkug". It's perfectly reasonable to reuse terms that already have meanings in a wider context. (This is just how language in general works.) Another point is that carving a personal distinction like this is a kind of naming, naming both sides of the distinction. Third, this is an example of the power of creating your own names, in the domain of emotions or personal experience.
The relationship to Chunking
Chunking is a hypothesis, or observation, from Cognitive Science. The keywords are "the magic number 7, plus or minus 2" (Miller 1956), and "Perception in chess" (Chase and Simon 1973). The idea is that people can hold a fixed number of "chunks" - such as words (which would be pretty information-dense, lots of bits in the ordinary computer representations) or digits (which is pretty information-fluffy, not many bits in the ordinary computer representations), in working memory. Which makes measuring working memory capacity, in bits, inappropriate.
In order to increase one's digit span (the number of digits you can hear and then recite back accurately), it is possible to deliberately memorize chunks such as pairs of digits or triples of digits. Someone who has pre-memorized all pairs of digits can still only hold 7±2 chunks in their working memory, but since their chunks are pairs of digits, that's 14±4 digits, so their digit span has increased. Someone who has pre-memorized all triples of digits might have a digit span of 21±6 digits.
Deciding to name some phenomenon or pattern means deciding to think in an internal language where that phenomenon or pattern exists as a basic entity. Shifting your internal language like that may make some things easier to think of, or to think with. I think the normal cost is simply opportunity cost, that deliberately memorizing chess chunks takes time that you could use to chunk something else, such as details of your beloved's sense of humor.
Guy Steele's "Growing a Language", Nand2Tetris and MHRD, Hierarchy
Guy Steele gave a talk in 1998 on "Growing a Language", which was amazing, more like a performance art piece than a talk. It starts out very strangely, and a viewer who doesn't know what the trick is already would be confused - "why is he talking so strangely?". After a while, if you're a programmer, you get a sense that he's written his talk like source code, with a lot of definitions building up to something. If you're particularly insightful, you might guess it, but he eventually builds up enough definitions to explain what he's doing directly. To spoil the trick, he defines every multi-syllable word he wants to use before using it. The weird feel of the talk very successfully conveys how a moderately large program feels, without requiring the listener to study a programming language in order to grok it.
In principle, you could draw a graph of each term in Guy Steele's talk, and link every "use" to the corresponding "def".
Nand2Tetris is a book, and MHRD is a computer game, but they're both similar feats. If you work through the Nand2Tetris book, or the MHRD game, then you will build an entire CPU up from basic elements. The basic gates are used to define components like registers and adders, and then those components are used to define bigger components like memory, arithmetic units, instruction decoders, and eventually the entire computer. Again, in principle, you could draw a graph of each component, and link every "use" to the corresponding "def".
"Cosmic View: The Universe in 40 Jumps", the book by Kees Boeke and the Eames's 1977 "Powers of Ten" video inspired by "Cosmic View", have a structure. The image at 100m scale contains (uses) the entire image at 10m scale, and so on. Again, in principle, you could draw a graph of the links between the 40 different scales, but it would just be a long chain of 40 uses and 40 defs. My point is that this graph is quite deep. If you were following some instructions for making some ordinary-sized object, like a vase, and the instructions had 40 levels of nesting canes within canes within canes, you would be skeptical. "Is anybody going to be able to tell the resulting cane apart from a solid-color cane?" you might have reason to ask. (Specifically, the universe cane would be essentially indistinguishable from a pure vacuum-colored cane).
Software, and computer hardware, and scientific and mathematical theories, all use abstractions, and it's true that in some ways Millefiori is like abstractions. However, an important difference to keep in mind is that these abstract domains routinely use quite deep nesting structures, deeper than glass or polymer clay construction procedures usually go. This is what I mean by the term "hierarchy".
This kind of hierarchy is not similar to a tree-shaped feudal structure where monarchs relate to large lords who relate to small lords who relate to relate to knights who relate to serfs. In such a tree shape, each person only has one liege that they owe fealty to, and so there has to be a lot of different serfs at the bottom of the tree. Rather, because of sharing/reuse, this kind of hierarchy is deep but hopefully narrow, particularly at the bottom layers. We expect there to be only a few kinds of basic elements. Only a few types of transistors or gates or whatever suffice to build the entire CPU or computer. Only a few kinds of elemental particles suffice to explain the entire universe, and so on.
In scientific diagrams, there's a graphical convention, a sort of zoom-in divergent or convergent pair of lines (depending on which way you're going), that is used in multiscale diagrams.
The meaning of these zoom-in lines is that on the narrow end of the zoom there is a "use", and on the wide end of the zoom is a "def".
Postscript: Haddock's Eyes
'You are sad,' the Knight said in an anxious tone: 'let me sing you a song to comfort you.'
'Is it very long?' Alice asked, for she had heard a good deal of poetry that day.
'It's long,' said the Knight, 'but very, VERY beautiful. Everybody that hears me sing it--either it brings the tears into their eyes, or else--'
'Or else what?' said Alice, for the Knight had made a sudden pause.
'Or else it doesn't, you know. The name of the song is called "Haddocks' Eyes."'
'Oh, that's the name of the song, is it?' Alice said, trying to feel interested.
'No, you don't understand,' the Knight said, looking a little vexed. 'That's what the name is called. The name really IS "The Aged Aged Man."'
'Then I ought to have said "That's what the song is called"?' Alice corrected herself.
'No, you oughtn't: that's quite another thing! The song is called "Ways and Means": but that's only what it's called, you know!'
'Well, what is the song, then?' said Alice, who was by this time completely bewildered.
'I was coming to that,' the Knight said. 'The song really is "A-Sitting on a Gate": and the tune's my own invention.'