Sometimes in order to refer to something, a complicated concept, you need to ask the listener to follow an imaginative recipe, a sequence of visualization operations. How does that work, in detail?
The colon operator
There is a visualization strategy which is commutative and associative, something like "please hold these several things in mind together". To be vivid about it, imagine an enthusiastic English lady, someone like Winifred Banks, the mother character from Mary Poppins, or Lady Carlotta from Saki's short story "The Schartz-Metterklume Method", shopping and handing various brown paper packages wrapped up with string to an obedient follower, gradually accumulating a humorously tall pile that conceals the follower's face. This concept corresponds to Margaret Masterman's ":" operator in the NUDE interlingua - but in the mathematics tradition, it might be more usual to use "+" for a basic commutative-associative operator like this.
Extrapolation
There is another visualization operator, which is often appropriate to use with the ":" operator. You might call it "description" or "extrapolation". It's similar to the three dots ellipsis operator in mathematics - given a sequence of examples followed by three dots, like "1, 1, 1, ..." or "1, 2, 4, 8, 16, ..." the reader is expected to use their own resources to imagine what extension the writer intended, with the understanding that the writer, ahead of time, has anticipated what extension the reader might be imagining, and has given all the necessary clues for the reader's initial guess as to what the writer intended to be correct. To be vivid about it, there's a metaphor (from the Surangama Sutra?) of a finger pointing at the moon.

Let's try and use these two operators together. There's a concept of a 2x2 diagram (I have previously written a little about 2x2s as "Conceptual Structures" ), or an a:b::c:d metaphor. The grapheme for lowercase letter t, written with a small rightward-turning tail, and the grapheme for lowercase letter f, written with a small rightward-turning ascender, might be recognized as having a mirror relationship with one another - if you were to look at a reflective pool of still water with one of these graphemes beyond it, then you might recognize the other of these graphemes in the surface of the water. Orthogonally, the lowercase letter t is the initial letter of the word "true" or "truth", and in some algebraic systems, someone might choose to use the letter to represent the word or the concept, in order to state sentences like "t & t = t". Parallel to the "t can mean truth", there is a "f can mean false" relationship. Between truth and falsehood there is a relationship of opposites or negation, which is different than the mirror symmetry, but which is similar to the mirror symmetry in that double negation yields the identity, just like double mirroring yields the identity. I would claim that this 2x2 diagram or a:b::c:d metaphor is a little bit redundant, or self-healing, or "a holographic self representation". That is, we can take any of the four (or eight, or nine, depending on how you like to count) elements, such as "the grapheme for lowercase letter t", and erase it, and use the rest of the 2x2 diagram to successfully refer to the erased concept.
In Margaret Masterman's NUDE, these descriptions of a concept by holding several familiar concepts together and then extrapolating or pointing to the missing concept might correspond to equations like this (the "/" operator is a noncommutative operator, with an intended meaning something like "the concept on the left, applied to the concept on the right").
tgrapheme = extrapolate / (fgrapheme : true : false)
fgrapheme = extrapolate / (tgrapheme : true : false)
true = extrapolate / (tgrapheme : fgrapheme : false)
talse = extrapolate / (tgrapheme : fgrapheme : true)
Maybe a better way of rendering these (counting the 2x2 diagram as having 8 elements) is:
tgrapheme = extrapolate / (fgrapheme : true : false : negation : mirrorsymmetry)
fgrapheme = extrapolate / (tgrapheme : true : false : negation : mirrorsymmetry)
true = extrapolate / (tgrapheme : fgrapheme : false : negation : mirrorsymmetry)
false = extrapolate / (tgrapheme : fgrapheme : true : negation : mirrorsymmetry)
negation = extrapolate / (tgrapheme : fgrapheme : true : false : mirrorsymmetry)
mirrorsymmetry = extrapolate / (tgrapheme : fgrapheme : true : false : negation)
Or you could include the entire concept of "a 2x2 diagram" to make 9 "packages" that the reader needs to hold onto.
Geometrization
There's a thing that you can do with some pairs, triples, and a:b::c:d 2x2 conceptual structures, transforming the conceptual structure into something smoother and more spatial. I think of this as "geometrization".
The vowel diagram
The vowel quadrilateral is a diagram with two axes, which we might call "high-low" and "front-back". The vowel in "bead" is both high and front. The vowel in "booed" is both high and back. The vowel in "bad" is both low and front. The vowel in "bawd" or "bod", which I pronounce as homophones, is both low and back.
We can gradually blend between "bead" and "bad", and recognize some of the intermediates as words - "bead", "bid", "bed", "bad". It takes a lot of work to figure out how to blend these in a way that causes the diagram to be successful, though in hindsight it seems obvious.
The circumplex model of affect
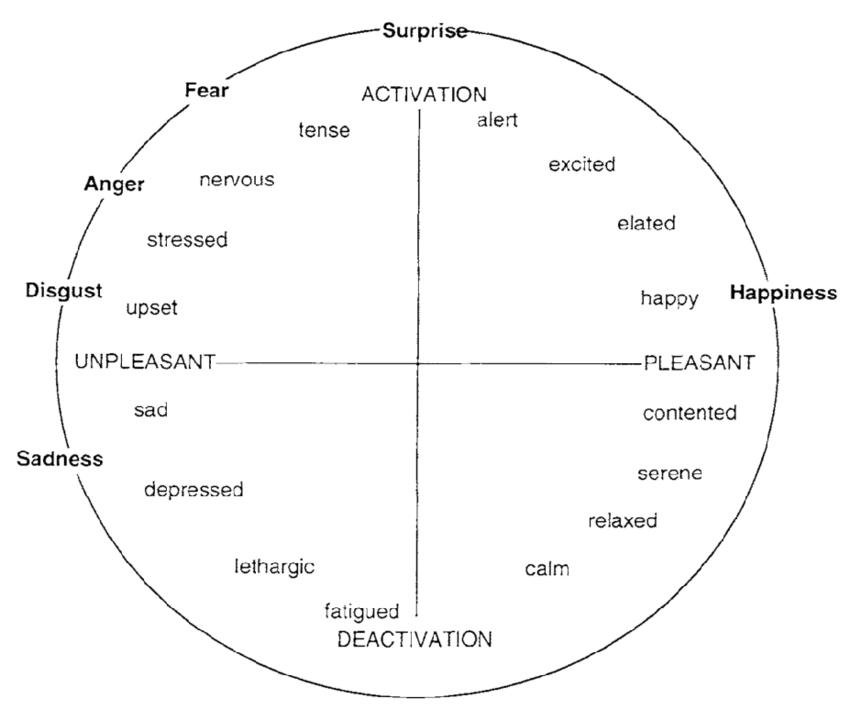
The circumplex model of affect is a diagram with two axes, called "high-low arousal" and "negative-positive valence". On the diagram we might put emotion words. In the "high arousal / negative valence" quadrant we might put words like "anxious". In the "high arousal / positive valence" quadrant we might put words like "happy" or "excited". In the "low arousal / negative valence" quadrant we might put words like "sad". In the "low arousal / positive valence" quadrant we might put words like "calm".
Both the vowel quadrilateral and the circumplex model of affect are examples of conceptual structures, and in particular, I described them as if they were 2x2s. But they're also examples of geometrization. The distinction is that these are not just four discrete concepts in parallel relationships to one another, but that it also makes sense to form a weighted blend between some or all of these concepts.
The 32-wind compass rose
There is a third example of geometrization, the 32-wind compass rose. Constructions like "north by east" indicate that you are referring to a direction that is a blend of north and east, but including lots of north and only a little east, while "north-northeast" means "an equal blend of north and northeast" (and of course "northeast" means "an equal blend of north and east").
Barendregt's Lambda Cube
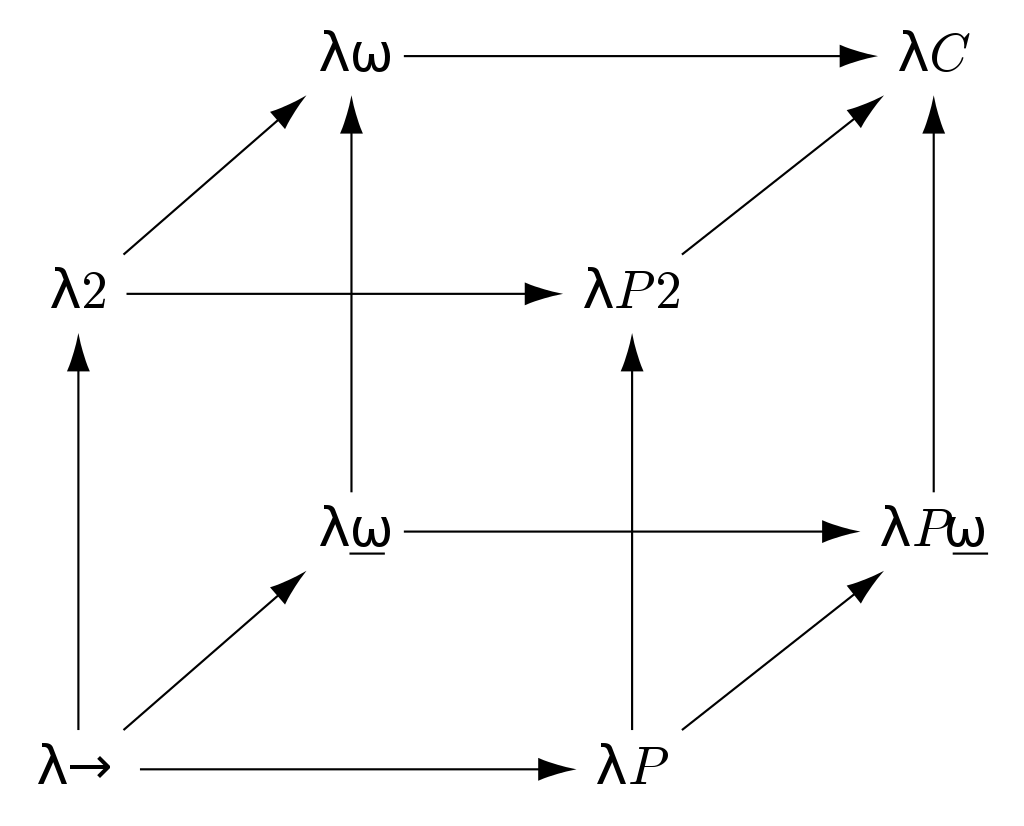
As a counterexample, Barendregt's Lambda Cube is a conceptual structure. It has 8 entities (logics) that relate to one another in three ways (axes). However, these are highly rigid, crisp, and complicated entities. It is at least difficult, if not impossible, to imagine constructing entities that are half-way blended between two or more of these entities. To apply geometrization to the lambda cube, you would have to be able to imagine constructing entities that are unequally blended between two or more of these.
Word Embeddings
Word embeddings are routinely used in natural language processing. These are constructed automatically, and therefore often have many more dimensions than manually-constructed embeddings. The fact that systematic techniques exist for constructing word embeddings make me think that geometrization is more generally applicable than it might at first seem.
External Reference
I am not too sure about how exactly this works, but if two entities (people) have some common background (such as a shared language and/or a movie that they have both seen) then it's possible for them to communicate. When I say "the sun" or "the character Doc from the movie Back to the Future" and you read that and understand what I'm referring to, the meaning is not established structurally, or at least it's not structural exclusively within this document. I'm leaning on our common background, and when an external reference has structure, it's similar to an address within that common background. "Terminal B Gate 5" is like a very short and simple program for navigating through an airport: Look at what terminal you are in, if you are not already in terminal B go "upstream" until you see signs for Terminal B, then follow those signs until you are in terminal B. Then, similarly, if you are not already in sight of Gate 5, go "upstream" until you see signs for Gate 5, then follow those signs until you are in sight of Gate 5.
These external references are often the leaves of visualization instructions, ur-elements that you can apply the colon operator or the extrapolation operator to.
Circumlocution
Circumlocution is related via Latin etymology to "talking around" something which sounds to me like someone was thinking geometry. Often it is valuable when pointing to a concept to give examples and counterexamples. Let's borrow the generic term "circumlocution", and re-use it as if it were a fresh or technical term within the context of this document to mean this particular kind of description. In order to refer to something via circumlocution we need to have a collection of entities - we can use the colon operator for that collection - and we also need to mark each entity as either a positive example or negative counterexample. Let's use "+" and "-" for that.
geometrizable = circumlocution / (+/vowel_diagram : +/circumplex_affect_model : +/compass_rose : -/lambda_cube)
Since we have to mark the examples and counterexamples anyway, we might also reuse the "pointing" operator instead of using a new circumlocution operator. However, there's nothing forcing that "simplification".
prime = pointing / (+/2 : +/3 : +/5 : +/7 : -/1 : -/4 : -/6)
polyhedron = pointing / (+/tetrahedron : +/cube : +/octahedron : +/dodecahedron : +/icosahedron)
It is quite usual when trying to securely refer to a concept, to make several different attempts to describe it, including some attempts that do not use circumlocution, and also at least one that does use circumlocution. To gesture at what this might look like in NUDE:
...some fresh term... = interpolate / ( pointing / (...some description…) : pointing / (...some other description...) : pointing / (...a third description...) : circumlocution / ( +/...example... : +/...example... : -/...counterexample... ) )
Pointing to a fresh term by giving multiple approximations, some more direct, and some circumlocutions using a set of examples and counterexamples, is particularly nice because if you have a sense of what the direct description is referring to, you can test that sense against the examples and counterexamples. On the other hand, when it is not clear how to generalize the examples and counterexamples to a concept, the
Interpolation
This talk about geometrization motivates a slightly different kind of "pointing", something like "interpolation". If you have several approximate descriptions, then you can say "It's somewhat like this, but also somewhat like that."
NE = interpolate / (N : E)
N-NE = interpolate / (N : NE)
NbE = interpolate / (N : N-NE)
You can use this construction with the circumplex affect model to explain your own emotions, saying "I feel somewhere between nervous and excited". In fact, the fresh or technical terms within the circumplex affect model like "arousal" and "valence" were described earlier only by reference to the example words. If you have several poor descriptions of something, you may be able to combine them together in order to point to something that is difficult to describe or to point to.
High-arousal = interpolate / (nervous : excited)
High-valence = interpolate / (excited : calm)
Low-arousal = interpolate / (sad : calm)
Low-valence = interpolate / (nervous : sad)