Previously, I talked about pinning down a network of concepts using definitions, descriptions, and examples. There are some other (lesser? secondary?) techniques that are also valuable to name.
Citation
The first is the citation. By "citation" I mean anything that directs the reader's attention out of the document, to the world; "fourth-wall-breaking". Often, this is to another document.
Citations can anchor a concept to the world outside the network-of-concepts, which is an amazingly powerful technique. The world is incredibly rich and it's also what we are usually interested in, which means pointing to a thing is a form of communication that is dense with relevant information.
A hyperlink to a different site can be a citation in some circumstances. A few keywords suggested to put into a search engine can be a citation. Academic citations might be to a particular article (keyed by title and page number) of a particular issue (keyed by date and/or number) of a particular journal (by name and publisher). One criterion to tell whether a span of text is a citation, is to ask whether it provides an intrinsically-meaningless dense route (or procedure) for the reader to follow (or execute), in the real world, to get to more matterial. The url in a link directs someone who has access to a browser and the internet to type the url into the address bar. Using keywords directs someone who has access to a search engine to search for those keywords. Academic citations are like directions for walking down aisles in a library.
However, citations are problematic. One of the ways that citations are problematic is the false impressions that citations are necessary or sufficient.
I hope I have already convincingly demonstrated that networks-of-concepts can get along without citations. Even without citations, a moderately rich network-of-concepts like Protocol Buffers syntax can still be itself. Adding a citation to, for example RFC 5234, the RFC that defines ABNF, can be beneficial, in precisely the same way that an additional definition, description, or example can be beneficial. Someone who is confused about some question may be able to obtain the referent of the citation, and then use it to answer their question. However, it can also be harmful, in exactly the same way that adding an additional definition, description, or example can be harmful - you can introduce confusion to something that was clear, or you can overwhelm with volume.
Citations are also not sufficient. One problem is that the reader may not have access to the referent of the citation; links break. Another problem is that the world changes. For example, citing RFC 5234 may be fairly clear now, but it obsoleted RFC 4234, and so we can imagine a future where other things obsolete your referent, which may turn what was initially very clear into a muddle. Citing a set of keywords is illustrative in that it might be more fragile or more robust. If your intent in citing that set of keywords is to pick out one particular document, then even though those keywords reliably pick out that document now, almost anything changing in the internet may cause that link to fail. If your intent was to point to a broad collection of similar documents (monad tutorials?), then the set of keywords may flex with the changing world and more durably refer to a representative member of your intent than a particular URL.
Elision
Elision is leaving something out. It is entirely reasonable for an author to not use all of the techniques for pinning down a concept. They may choose to describe one thing, provide a few examples of another thing, and define a third thing. More is not always better.
As a reader, the possibility of elision enormously affects the reading process. If the task of reading one of these documents-that-describe-networks-of-concepts was primarily categorizing any span of text according to which concept it is trying to pin down now, using which technique, then the size of the reading task would be closely related to the size of the text. However, if the author can lean on the whole of the reader's competence to fill in any and all gaps, then the size of the reading task can only be bounded by the reader's competence.
Sometimes authors leave elision markers in documents. The ellipsis "..." is an elision marker. The phrase "... left as an exercise for the reader." is an elision marker. Also, "Of course", "Trivial", "Clearly" and "Obviously" are sometimes elision markers.
Arguments
The best way I have to explain arguments is by reference to a different idea, of informal proofs. Informal proofs are networks of declarative claims (sentences), that are connected together by a "these sentences here together support that sentence" relationship. The standard example (maybe from Aristotle's Prior Analytics?) is "All men are mortal." and "Socrates is a man.", taken together, support "Socrates is mortal.". There are three declarative claims, and they're connected together in a little triangle or tree shape.
There are two rules for evaluating informal proofs: the hand-holding rule and the rabbits rule. In order for "All men are mortal" and "Socrates is a man" to be used together, they need to "hold hands" - meaning that they have to have a common concept, in this case "men". That's the "hand-holding" rule.
The "rabbits" rule is that you can't get a concept in the conclusion that wasn't anywhere in the premises. In "Socrates is mortal", the concept "Socrates" came from one of the premises, and "mortal" came from the other.
Note that I am not trying to argue that informal proofs are proofs, or that they necessarily correct or anything. I'm simply claiming that they "hang together" in a "no obvious fallacies of relevance" manner.
Arguments are informal proofs, plus elisions. That is, they are sets of declarative claims, that the author believes the reader can elaborate into an informal proof.
Let's try to create an example of an informal proof, and then elide pieces of it to create an example of an argument.
Kakuro is a game like a crossword, but instead of being filled out with letters, the horizontal and vertical spans are filled out with the digits one through nine. In crosswords, the spans must be filled with real words. In Kakuro, the spans must follow a different rule - they cannot contain multiple of any digit. Finally, for each span in a crossword there is a clue (connected to the grid via a numeric index). In Kakuro, the numbers associated with each span are the clues - specifically, they are the totals.
Before looking at a specific puzzle, let's look generically at a single span. It has a number of boxes and a total. Some combinations, like a total of 1 from 2 boxes, are impossible; any way to assign 1-9 into both of those boxes will add up to greater than 1. Other combinations are impossible at the other extreme; making a total of 50 from 2 boxes are equally impossible. In between those extremes, there is a sort of hump shape. First there are totals that are minimal for the number of boxes, such as a total of 3 for 2 boxes, then there are totals that have many ways to be met (a total of 10 for 2 boxes could be 4 and 6, 3 and 7, 2 and 8, or 1 and 9). Then there are totals that are maximal for the number of boxes, such as a total of 17 for 2 boxes, which can only be met by 8 and 9.
Now let's look generically at two intersecting spans. If one of the spans has a minimal or near-minimal total, and the other has a maximal or near-maximal total, then it may be that there is only one possible digit that can fill the intersection. For example, a total of 15 across 5 boxes is minimal, and can only be made from 1+2+3+4+5. A total of 35 across 5 boxes is maximal and can only be made from 5+6+7+8+9. So if those two spans intersect, then we can conclude that the digit in the intersection is 5.
So now let's look at this puzzle:
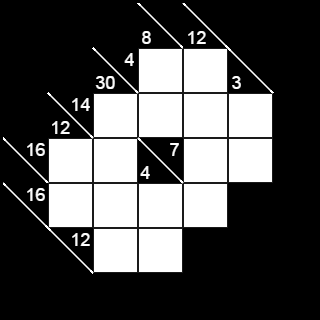
At the bottom of the puzzle, there is a vertical span of 2 boxes with a total of 4. It intersects a horizontal span of 2 boxes with a total of 12. There is only one way (in Kakuro) to make a total of 4 from 2 digits: 1+3. There are several ways to make a total of 12 with 2 boxes, but none of them include 1. So the digit at the intersection of those spans must be 3:
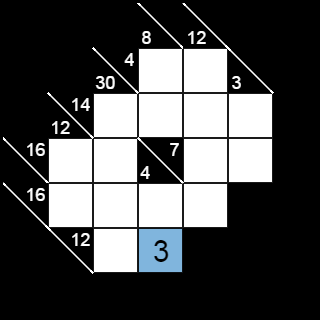
Consequently, the remaining box in the vertical span must be 1, and the remaining box in the horizontal span must be 9.
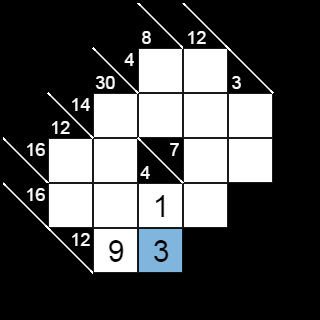 .
.
To be obsessively precise about this, the informal proof goes something like this:
- Given: this particular puzzle.
- Given: the rules of Kakuro.
- There is a vertical span of 2 boxes with a total of 4. (From 1)
- Those boxes will be filled with the digits 1 and 3. (From 2 and 3)
- There is a horizontal span of 2 boxes with a total of 12. (From 1)
- Those boxes will be filled with the digits 5 and 7 or 4 and 8, or 3 and 9. (From 2 and 5)
- The intersection box will be filled with 3. (From 4 and 6)
- The other box in the vertical span will be filled with 1. (From 4 and 7)
- The other box in the horizontal span will be filled with 9. (From 6 and 7)
Still behaving obsessively, we can check that this is an informal proof:
- The supports relationship of 1 to 3 is rabbit-correct because they share the concept of that particular vertical span. There is no other claim that together supports 3 so it is also holding-hands-correct.
- The supports relationship of 2 and 3 to 4 is holding-hands-correct because 2 and 3 share the concept of a generic span of 2 boxes with a total of 4. The concept in 4 of "will be filled with the digits 1 and 3" comes from 2. The concept, in 4, of those particular boxes comes from 3. So the supports relationship of 2 and 3 to 4 is also rabbit-correct.
- The supports relationship of 1 to 5 is correct analogous to the supports relationship of 1 to 3.
- The supports relationship of 2 and 5 to 6 is correct analogous to the supports relationship of 2 and 3 to 4.
- The supports relationship of 4 and 6 to 7 is holding-hands-correct because 4 and 6 share the concept of that intersection box. The concept of that box being filled with 3 comes from 7 (redundantly, it also comes from 6). So the supports relationship of 4 and 6 to 7 is rabbit-correct.
- The supports relationship of 4 and 7 to 8 is holding-hands-correct because 4 and 7 share the concept of that box being filled with 3. The concept of the other box in the vertical span being filled with 1 comes from 4, so the the supports relationship of 4 and 7 to 8 is also rabbit-correct.
- The supports relationship of 6 and 7 to 9 is correct analogous to the supports relationship of 6 and 7 to 9.
Lots of different arguments can be made, eliding different parts of this informal proof. To an expert Kakuro player, all of these probably seem tedious. Arbitrarily skipping every other line, we might get an argument something like this:
- Given: this particular puzzle.
- Observe there is a vertical span of 2 boxes with a total of 4.
- Observe there is a horizontal span of 2 boxes with a total of 12.
- Clearly, the intersection between them can only be filled with 3.
- So the other box in the horizontal span will be filled with 9.
In more difficult arguments, we can't choose arbitrarily which parts to elide - as an author, we need to decide whether to elide, based on whether it would be more effective to request the reader to reconstruct the elided parts. Elision makes the text shorter, which is amazingly helpful - there are all kinds of synergetic beneficial to making a text shorter and/or simpler, but it can also make the text more difficult.
As a reader, it is sometimes helpful to lean on the holding-hands rule and the rabbit rule in order to reconstruct an informal proof from an argument. If a conclusion, C, seems to be derived from a syntactically disjoint (syntactically irrelevant) premise, P, then the simplest elided claim that passes the holding-hands rule and the rabbit rule is generally of the form "If P then C" (I believe Toulmin calls these kinds of claims "warrants"). These claims are particularly nice to elide because they are verbose and easy for the reader to reconstruct (particularly if the reader is familiar with the holding-hands rule and the rabbit rule).